Artikel Kopfzeile:
Zahlen, Daten, Diagramme
So durchschaust du jede Statistik
Statistik und Lüge werden oft in einen Topf geworfen. Das ist falsch. Denn Statistiken können viele nützliche Informationen liefern – solange sie richtig interpretiert werden. Ein Überblick.
Sprungmarken des Artikels:
Inhalt
- Ab wann ist eine Studie repräsentativ?
- Was beeinflusst die Antworten in Umfragen?
- Korrelation ist nicht gleich Kausalität!
- Wann ist ein Ergebnis signifikant?
- Was ist besser – Median oder Mittelwert?
- Wie kann man mit Grafiken Statistiken verfälschen?
- Warum sind absolute Zahlen problematisch und wichtig?
- Ab wann ist eine Studie repräsentativ?
- Was beeinflusst die Antworten in Umfragen?
- Korrelation ist nicht gleich Kausalität!
- Wann ist ein Ergebnis signifikant?
- Was ist besser – Median oder Mittelwert?
- Wie kann man mit Grafiken Statistiken verfälschen?
- Warum sind absolute Zahlen problematisch und wichtig?
Weitere Angaben zum Artikel:
Die wichtigsten Statistikbegriffe
Stichprobe
Ist eine Auswahl an Objekten, die stellvertretend für eine Grundgesamtheit oder Zielpopulation steht.
Konfidenzintervall
Ist die Spanne zwischen den Fehlergrenzen in die positive und negative Richtung.
Lotterieeffekt
Davon ist die Rede, wenn sich – etwa bei einer Umfrage – Menschen mit einer bestimmten Meinung in der Stichprobe zufällig häufen.
Suggestivfragen
Fragen, die durch ihre Wortwahl nicht neutral sind, sondern dem Befragten Antworten in den Mund legen oder ihm eine Ahnung davon geben, was der Interviewer hören will.
Korrelation
Gibt wieder, wie stark zwei Variablen statistisch in Beziehung stehen. Eine positive Korrelation heißt: je mehr Variable A, desto mehr Variable B (und umgekehrt); eine negative Korrelation heißt: je mehr Variable A, desto weniger Variable B (und umgekehrt).
Kausalität
Wenn zwei Merkmalen so zusammenhängen, dass man sie als Ursache und Wirkung verknüpfen kann, spricht man von Kausalität.
Artikel Abschnitt: Ab wann ist eine Studie repräsentativ?
Ab wann ist eine Studie repräsentativ?
So stand es im Herbst 2020 in einigen Zeitungen. Der Hintergrund: Für den ARD-Deutschlandtrend sind Menschen in ganz Deutschland nach ihrer Meinung zu Karneval und Weihnachtsmärkten während Corona befragt worden. Aber natürlich nicht alle Menschen in Deutschland, sondern nur um die 1000 Personen. Kommentare auf Facebook zu solchen Schlagzeilen kann man eigentlich schon vorhersagen: "So so! Alle Deutschen, ja? Also mich hat keiner angerufen und gefragt! Wie soll denn diese Umfrage aussagekräftig sein?"
Durchaus klingt es eigenartig, dass eine Gruppe von 1000 die Meinung von 81 Millionen widerspiegeln soll.
Warum also gilt eine solche Umfrage trotzdem als repräsentativ?
Stichprobe sagen Statistiker dazu, wenn sie sich einen kleinen Teil einer großen Gruppe herausgreifen, um einer bestimmten Fragestellung nachzugehen. Das können wir uns vorstellen wie beim Kochen: Angenommen wir haben einen großen Eintopf auf dem Herd stehen und wollen probieren, ob er genug Salz hat. Es wäre übertrieben, den ganzen Topf leer zu löffeln, stattdessen probieren wir einen kleinen Teil von einer zufälligen Stelle im Topf. Haben wir vorher genug umgerührt, können wir also davon ausgehen, dass das Salz gleichmäßig im Topf verteilt ist. Dann stehen auch die Chancen gut, dass dieser Klecks Eintopf auf dem Löffel genauso würzig schmeckt wie der Rest der Suppe.
Eine gute Studie zeichnet sich dadurch aus, dass die Gruppe der Untersuchten – also die Stichprobe – zufällig aus der gesamten Zielpopulation ausgewählt wurde. Die Zielpopulation, das sind alle Individuen, auf die sich die Fragestellung bezieht. Das können Menschen sein oder eine bestimmte Tierart, eine Gruppe Pflanzen, Gesteinsbrocken – oder was auch immer der Beobachtungsgegenstand der Studie sein soll.
Doch Stichproben können verzerrt sein
Der Mathematiker Karl Bosch hat in seinem Buch "Statistik – Wahrheit und Lüge" ein anschauliches Beispiel geliefert, wie falsche Stichproben zustande kommen können und was das mit einer Untersuchung machen kann. Dazu erzählt er von einem Krebsforschungsinstitut, in dem Versuche an Ratten durchgeführt wurden. Welche Versuche genau das sind und welche Ergebnisse dabei herauskommen sollten, erklärt Bosch nicht näher. Nur so viel: Immer, wenn die Forscher ihre Daten statistisch durchrechneten, machten die Ergebnisse keinen Sinn. Sie ließen sich nicht auf die Gruppe aller Ratten übertragen.
Was war passiert? Die Forscher hatten für ihre Versuche zehn beliebige Ratten aus den Käfigen für ihre Versuche ausgewählt. Sie hatten sich dabei das erstbeste Tier gegriffen, das in der Nähe der Käfigtür saß. Klingt sehr zufällig. Ist es aber nicht, denn die Ratten gleich neben der Käfigtür waren offenbar krank und nicht mehr in der Lage, wegzurennen. Die Stichprobe war verzerrt.
Ein Statistiker schlug vor, die Tiere durchzunummerieren und zu kennzeichnen und aus den Zahlen eine zufällige Auswahl zu treffen, etwa mithilfe eines Computers. So hatte jedes Tier die gleiche Chance in den Versuch aufgenommen zu werden – eine tatsächlich zufällige Stichprobe. Und das ist wichtig, denn: Zufällige Stichproben dürfen nicht systematisch bestimmte Gruppen in der Zielpopulation einschließen oder ausschließen.
Das lässt sich genauso auf Befragungen anwenden: Ebenfalls in Boschs Buch gibt es ein anderes Beispiel von zwei Schülergruppen, die die Aufgabe hatten, jeweils 200 Erwachsene nach ihrem Schulabschluss zu fragen.
- Die eine Gruppe erzielte das Ergebnis, dass 89 Prozent der Befragten Abitur hatten.
- Die andere Gruppe fand heraus, dass 12 Prozent der Befragten Abitur hatten.
Wie diese Kluft zustande kam? Die eine Gruppe hatte ihre Befragung in der Nähe einer Uni durchgeführt, die andere hatte Menschen vor einem Supermarkt befragt. Solche Fehler in der Versuchsplanung können die kompletten Untersuchungsergebnisse verzerren. Deshalb ist es immer nützlich zu wissen, wie die Stichprobe zustande gekommen ist.
Die Grenze von 1000
Gerade bei Umfragen heißt es oft: 1000 Menschen wurden befragt, deshalb ist diese Umfrage repräsentativ. "Repräsentativ" bedeutet, dass sich aus dieser kleinen Gruppe von Befragten zutreffende Rückschlüsse auf eine große Grundgesamtheit ziehen lassen (zum Beispiel alle Einwohner Deutschlands). Die Voraussetzung: Alle Angehörigen der Grundgesamtheit (also etwa alle 80 Millionen Deutschen) hatten die gleiche Chance, Teil dieser Stichprobe zu sein. Erst dann gilt die Stichprobe als zufällig gewählt – und repräsentativ.
Wenn eine Stichprobe wirklich zufällig erstellt wurde, kann sie ab einer bestimmten Größe ein Bild über die gesamte Zielpopulation abgeben. Es gibt in der Statistik eine Faustformel, mit der sich berechnen lässt, wie genau eine Stichprobe die Grundgesamtheit abbildet, über die man etwas herausfinden möchte. Die Faustformel misst sich an der Größe der Stichprobe. Dafür teilt man durch die Wurzel der Stichprobengröße.
Beispiel: Eine Befragung von 1000 Personen hätte damit eine Genauigkeit von 1/√1000 (eins geteilt durch Wurzel aus 1000).
Die Genauigkeit beträgt also 0,032. Und weil das nicht besonders aufschlussreich ist, kann man auch sagen, dass diese Stichprobengröße eine Fehlergrenze oder Fehlertoleranz von 3,2 Prozent aufweist. Das heißt also, dass das Ergebnis der Stichprobe um höchstens 3,2 Prozent von den Ergebnissen abweicht, die man in der gesamten Zielpopulation erfassen würde. Die 3,2 Prozent in die positive sowie in die negative Richtung nennt man übrigens Konfidenzintervall.
Je größer die Stichprobe, desto kleiner wird der Wert der Fehlergrenze – und umso genauer die Umfrage. Aber selbst bei viel größeren Stichproben sinkt er nicht auf null. Drei Beispiele:
- Eine Stichprobe von 2000 hätte eine Fehlergrenze von 2,2 Prozent.
- Eine Stichprobe von 10.000 hätte eine Fehlergrenze von 1 Prozent
- Eine Stichprobe von 100.000 hätte eine Fehlergrenze von 0,3 Prozent
Aber dafür müssten Forscher und Forscherinnen eben auch 100.000 Leute auswählen und befragen, was ein großer zeitlicher und finanzieller Aufwand wäre. Selbst eine Studie mit der größten Stichprobe kann die Realität also nie zu 100 Prozent abbilden, aber sie nähert sich ihr so gut es geht an.
Der Lotterie-Effekt
Trotz niedriger Fehlergrenzen gibt es die Macht des unglücklichen Zufalls, da kann die Stichprobe noch so zufällig gewählt sein. Statistiker sagen "Lotterieeffekt" dazu. Ist die Stichprobe gemessen an der Zielpopulation recht klein (zum Beispiel 1000 Befragte für eine Fragestellung, die sich auf 81 Millionen Deutsche bezieht), so kann der Zufall dazu führen, dass sich, etwa bei einer Meinungsumfrage, Menschen mit einer bestimmten Meinung in der Stichprobe häufen.
Der Mathematiker Gerd Bosbach und der Historiker Jens Jürgen Korff beschreiben das in ihrem Buch "Echt gelogen": "So wie ein Käufer aus einer Lostrommel, die zehn Prozent Gewinnlose enthält, mit sieben Losen zwei Gewinne erwischt, während ein anderer mit zehn Losen zehn Nieten zieht. Aufgrund dieses Lotterieeffektes dürften Meinungsforscher das Ergebnis der Stichprobe nicht einfach als Ergebnis auf die Gesamtbevölkerung übertragen, sondern müssten Angaben zur Unsicherheit der Hochrechnung ergänzen." In der Realität passiert das selten. Erinnern wir uns an das Deutschlandtrend-Beispiel vom Anfang: Wenn in den Schlagzeilen vieler Medien steht "Mehrheit der Deutschen für Absage von Karneval und Weihnachtsmärkten wegen Corona“, müssten die Autoren und Redakteure eigentlich noch hinzufügen, welche Unsicherheiten diese Ergebnisse bergen. Und dass es gut sein könnte, dass zufällig überwiegend Karnevals- und Weihnachtsmarkt-Muffel in der Stichprobe gelandet sind. Klingt dann halt nicht mehr so griffig.
Warum nichtrepräsentative Umfragen trotzdem spannende Statistiken ergeben können
Mal angenommen ein Forscher möchte wissen, wie Männer in Deutschland einkaufen. Dafür stellt er sich für zwei Monate jeden Tag vor einen Supermarkt in Bonn und befragt jeden Mann, der den Supermarkt verlässt. Seine Ergebnisse taugen natürlich nicht dazu, dass Kaufverhalten deutscher Männer abzubilden. Sie taugen nicht einmal dazu, das Kaufverhalten Bonner Männer abzubilden. Er wird aber vielleicht (wenn er seine Fragen richtig gestellt hat, dazu gleich mehr) erfahren, wie die Männer aus der Nachbarschaft den Einkauf in diesem Supermarkt empfinden.
Wer sich für das Kaufverhalten aller Männer in Deutschland interessiert, kann mit dieser Befragung nichts anfangen. Der Supermarkt aber, der vielleicht mehr Männer in seine Filiale locken möchte, findet die Ergebnisse sehr interessant. Ein Untersuchungsergebnis, das für eine gewisse Gruppe nicht repräsentativ ist, kann mit einer neuen Perspektive doch an Aussagekraft gewinnen.
In einigen Fällen ist es gar nicht möglich, repräsentative Stichproben zu sammeln
Ein Beispiel sind Studien im Schlaflabor. Dort untersuchen Forscherinnen und Forscher alles Mögliche: Wie sich Schlafmangel auf die Konzentration auswirkt, wie sich die Hirnaktivtität in bestimmten Schlafphasen verhält, welche Reize das schlafende Gehirn empfangen kann und vieles mehr. Das sind Fragestellungen, die vermutlich die meisten von uns interessieren, also wäre es wünschenswert, Ergebnisse zu bekommen, die für die ganze Gesellschaft gelten.
In der Praxis ist das aber fast unmöglich. Die Probandinnen und Probanden müssen dafür im Schlaflabor übernachten, manchmal gehen die Versuche mehrere Tage. Es ist ziemlich unrealistisch, 1000 zufällig ausgewählte Versuchspersonen aus der Gesamtbevölkerung zu finden, denen man einfach so sagen könnte: "Du gehst jetzt für zwei Wochen ins Schlaflabor." Schlafstudien sind deshalb viel kleiner. Meist bestehen sie nur aus ein paar Dutzend Probanden und das sind Freiwillige, die einem Aufruf gefolgt sind. Das macht die Untersuchungen nicht wertlos, man muss diese Umstände nur im Hinterkopf behalten, wenn man die Ergebnisse betrachtet.
Artikel Abschnitt: Was beeinflusst die Antworten in Umfragen?
Was beeinflusst die Antworten in Umfragen?
"Wenn die Zielpopulation beispielsweise aus Personen mit einer Sehbehinderung besteht, ist es ziemlich sinnlos, ihnen einen Fragebogen zuzusenden. Wenn Sie eine Umfrage über Opfer häuslicher Gewalt durchführen wollen, sollten Sie die Befragten nicht bei sich zu Hause aufsuchen."
Manchmal entscheidet der Wortlaut der Frage über die Antwort
Ein kritischer Blick auf die Durchführung kann sich also lohnen. Ebenfalls interessant ist die Art und Weise, wie die Fragen gestellt wurden. Ein großes Problem sind etwa Suggestivfragen. Also Fragen, die so formuliert sind, dass sie dem Befragten eine Antwort in den Mund legen, sodass er oder sie ablesen kann, welche Antwort erwartet wird.
- Wenn die neutrale Frage lauten würde: "Sind Sie für oder gegen das bedingungslose Grundeinkommen?", dann wäre ein Beispiel für eine Suggestivfrage: "Sind Sie für das bedingungslose Grundeinkommen, um eine freie Entfaltung für alle gewährleisten zu können?"
- Eine neutrale Frage wäre: "Sind Sie für oder gegen das Tempolimit auf Autobahnen?" Eine Suggestivfrage wäre "Sind Sie nicht auch für das Tempolimit, um damit eine größere Verkehrssicherheit und einen gleichmäßigen Verkehrsfluss zu erzielen?"
Das heißt: Werden in Studien Suggestivfragen gestellt, muss man damit rechnen, dass die oder der Befragte die Frage nicht nach der eigenen Meinung beantwortet. Am Ende führt das zu verzerrten Ergebnissen, die nicht die Realität abbilden.
Artikel Abschnitt: Korrelation ist nicht gleich Kausalität!
Korrelation ist nicht gleich Kausalität!
Weitere Angaben zum Artikel:
Definition: Korrelation
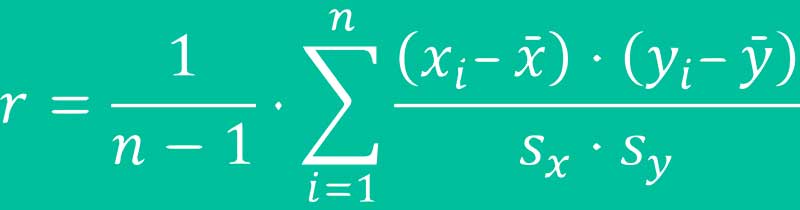
Der Korrelationskoeffizient nimmt immer einen Wert zwischen –1 und +1 an. Je näher er an –1 oder +1 herankommt, desto stärker stehen diese Variablen in Beziehung zueinander. Läuft der Korrelationskoeffizient gegen +1, spricht man von einer positiven Korrelation, läuft er gegen –1, ist es eine negative Korrelation.
Artikel Abschnitt:
Eine negative Korrelation bestünde zum Beispiel zwischen den gefahrenen Kilometern, die ein Gebrauchtwagen auf dem Buckel hat, und seinem Kaufpreis. Mit steigendem Kilometerstand sinkt der Preis, da mehr gefahrene Kilometer in der Regel auf den Wert des Fahrzeugs drücken.
Der Unterschied zur Kausalität
Dass eine Korrelation besteht, heißt aber nicht grundsätzlich, dass sich auch eine Kausalität finden lässt – also das sich die Variablen tatsächlich beeinflussen. Ein bekanntes Beispiel ist die Legende von den Störchen, die Babys bringen. So haben Beobachtungen ergeben, dass in Gegenden, in denen es viele Störche gibt, auch viele Babys zur Welt kommen. Wer zwischen den beiden Variablen einen Kausalzusammenhang herstellt, kann zu dem Ergebnis kommen, dass die Störche die Ursache für die Babys sind. Was natürlich Quatsch ist – und sobald man sich nach einer dritten Variablen umschaut, die beide – also die Zahl der Störche und die Geburtenrate beeinflusst – zerfällt die Geschichte vom Baby bringenden Storch. Denn je nachdem, wie industrialisiert eine Region ist, sinken oder steigen sowohl Geburtenraten als auch Storchvorkommen – ohne dass die Störche direkt was mit den Babys zu tun haben.
Kausalzusammenhänge, die zufällig auftreten, aber nichts miteinander zu tun haben, werden leider immer wieder aus Korrelationen geschlussfolgert. Der Grund: Nicht immer ist eine dritte Variable verfügbar, um die Korrelation zu erklären. Manchmal sind Korrelationen auch schlicht Zufälle.
Darum ist es wichtig, auf versteckte Variablen zu achten
Hinter "versteckten Variablen" verbergen sich nicht besonders hinterlistige Einflussfaktoren, die man erst nach langer Suche findet. Es handelt sich vielmehr um Variablen, auf die man ganz natürlich stoßen wird, je umfassender man sich mit allen Aspekten beschäftigt, die der zu untersuchende Datensatz haben kann.
Hätte man im Fall der Störche daran gedacht, dass die Vögel bevorzugt in ländlichen Regionen nisten und hätte man dann die Geburtenraten vom Land mit denen der Stadt verglichen, wäre die Legende wahrscheinlich nie entstanden. Denn es wäre klar gewesen: Die Variable, die sowohl mit der Storchpopulation als auch mit der Geburtenrate zusammenhängt, ist der Industrialisierungsgrad einer Region.
Ein anderes Beispiel, das den Einfluss versteckter Variablen veranschaulicht, kommt vom Datenportal Statista:
"In einer (fiktiven) Studie wird für verschiedene Berufe erfasst, in welchem Alter die Personen dieser Berufsgruppe im Schnitt sterben. Das Ergebnis der Studie ist überraschend. Während Piloten und Berufsfußballer im Schnitt mit unter 60 Jahren sterben, leben Lehrer und Mediziner deutlich länger. Was ist die Ursache? Gefährliche Arbeitsbedingungen, zu viel Stress auf dem Fußballplatz, zu viele Flugunfälle? Nein. Der Grund ist, dass hier Berufsgruppen miteinander verglichen werden, die keinen direkten Vergleich erlauben, weil eine dritte Variable (neben Beruf und Lebensalter) die Untersuchung stört: das Durchschnittsalter."
Weiter steht dort, dass es echte Berufsfußballer erst seit den 60er-Jahren gebe. Zudem sei die Flugbranche in den vergangenen Jahren stark gewachsen. Die Folge: viel mehr junge Piloten und Berufsfußballer als junge Lehrer und Ärzte. Sterben nun Fußballer oder Piloten jung durch Unfall oder Krankheit, fallen sie stärker ins Gewicht. Denn ihnen stehen weniger Fälle in ihrer Berufsgruppe gegenüber, die in hohem Alter sterben.
Nicht verwechseln: Korrelation und Assoziation
Die Korrelation gibt an, wie stark die Beziehung zweier quantitativer Variablen zueinander ist. Um die Beziehung zweier qualitativer Variablen zueinander zu beschreiben, nutzt man die Assoziation. Will man zum Beispiel vergleichen, ob Mitarbeitende nach dem Urlaub zufriedener sind als vor dem Urlaub, kann man das mit einer Befragung tun und beispielsweise den Prozentsatz der Zufriedenen vor dem Urlaub mit dem Prozentsatz der Zufriedenen danach vergleichen. Ist die Zufriedenheit nach dem Urlaub deutlich erhöht, kann man von einer Assoziation sprechen: Urlaub zu machen ist mit einer erhöhten Mitarbeiterzufriedenheit assoziiert.
Artikel Abschnitt: Wann ist ein Ergebnis signifikant?
Wann ist ein Ergebnis signifikant?
Dazu gibt es ein gutes Beispiel der Statistikerin Deborah Rumsey: Wenn eine Pizzakette behauptet, ihre Pizzen in weniger als 30 Minuten zuzustellen, ist das die Nullhypothese, die es nun zu überprüfen gilt.
Dabei hilft der p-Wert: Er spiegelt wider, inwiefern die erhobenen Daten die Nullhypothese stützen oder nicht. Er liegt zwischen 0 und 1:
- Je kleiner der p-Wert, desto mehr spricht das gegen die Nullhypothese.
- Je größer der p-Wert, desto weniger spricht er gegen die Nullhypothese.
Im Fall der Pizzakette würde man nun eine Zufallsstichprobe von beispielsweise 100 Zustellungen ziehen und die durchschnittliche Lieferzeit messen. Angenommen, die durchschnittliche Lieferzeit liegt bei 40 Minuten. Damit liegt sie mehr als zwei Standardabweichungen über der angekündigten Lieferzeit (weniger als 30 Minuten). Der p-Wert wäre klein und wir würden sagen, dass wir starke Beweise gegen die Behauptung der Pizzakette besitzen.
Das Problem: Statistisch signifikante Ergebnisse sind interessant, werden aber oft aufgebauscht. Erst wenn Folgestudien die Ergebnisse wiederholen können, sollte ihnen Bedeutung beigemessen werden – denn auch signifikante Ergebnisse können Fehler bergen, etwa wenn die Stichprobe zufällig verzerrt ist.
Wofür die Standardabweichung steht
Die Standardabweichung zeigt, wie stark die Werte der Stichprobe um den Mittelwert streuen. Sie ist grob gesagt der durchschnittliche Abstand vom Mittelwert. Die meisten Werte liegen in diesem Streubereich.
Sie ist eine wichtige statistische Kenngröße, die jedoch oft nicht angegeben wird. Fehlt die Standardabweichung, kann man sich eigentlich kein umfassendes Bild von den vorliegenden Daten machen. Der Durchschnittspreis für ein Haus in Deutschland sagt beispielsweise gar nichts über die Bandbreite an Hauspreisen aus. Das ist so, als stünde man mit einem Fuß in einem Eimer mit eiskaltem und mit dem anderen Fuß in einem Eimer mit kochendem Wasser und würde sagen, die Wassertemperatur sei im Durchschnitt perfekt. Erst die Standardabweichung macht das Spektrum der Hauspreise deutlich.
Artikel Abschnitt: Was ist besser – Median oder Mittelwert?
Was ist besser – Median oder Mittelwert?
- Der Mittelwert, auch das arithmetische Mittel genannt, ist die Summe aller Daten geteilt durch ihre Anzahl. Er liefert einen guten Überblick über einen Datensatz, ist aber nicht robust gegen Ausreißer. Darunter versteht man einzelne Daten, deren Wert vom Durchschnitt der übrigen abweicht.
- Der Median kann da mitunter helfen. Er entspricht dem Wert, der genau in der Mitte eines Datensatzes liegt, nachdem man alle Daten der Größe nach sortiert hat. Grob gesagt ist die Hälfte der Daten kleiner und die andere Hälfte größer als der Median. Liegen zwei Zahlen genau in der Mitte, weil der Datensatz eine gerade Anzahl an Werten enthält, nimmt man die beiden mittleren Werte, addiert sie und teilt sie durch zwei.
Artikel Abschnitt: Wie kann man mit Grafiken Statistiken verfälschen?
Wie kann man mit Grafiken Statistiken verfälschen?
Dort lohnt es sich, die Beschriftungen der Achsen genau anzuschauen und zu erfassen, wo die Achsen beginnen: Starten sie nicht bei null? Ändert das etwas am Gesamteindruck der Grafik?
Wer die Grafik erstellt, kann den Maßstab verändern und dafür sorgen, dass Unterschiede dramatischer aussehen und so Werte übertrieben darstellen. Mit einem größeren Maßstab etwa können Unterschiede kleiner dargestellt werden, als sie sind: Werte wirken harmloser, kleine Unterschiede können sogar unsichtbar werden.
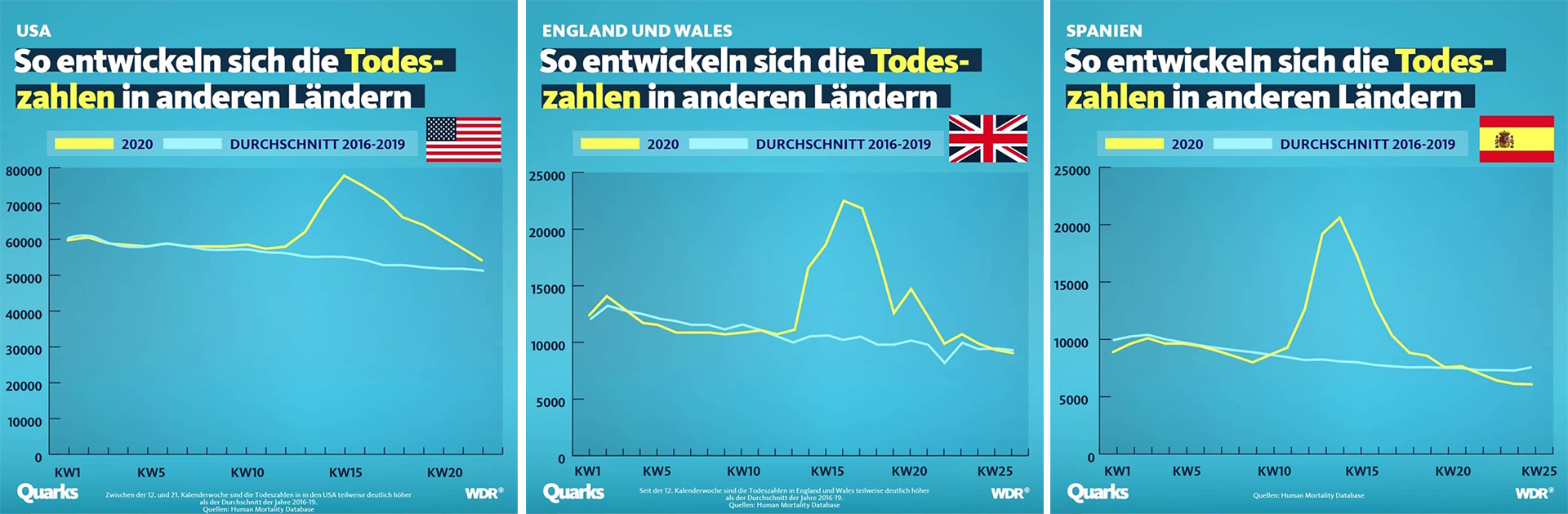
Ein Beispiel: In unseren Grafiken zu Corona-Toten in anderen Ländern sind die Werte der y-Achsen nicht überall gleich gewählt. Wer nicht genau hinschaut, könnte den Eindruck bekommen, in Großbritannien hätte es einen ähnlichen Anstieg wie in den USA gegeben. Dabei starten der zweite und dritte Graph auf der y-Achse viel früher.
Artikel Abschnitt: Warum sind absolute Zahlen problematisch und wichtig?
Warum sind absolute Zahlen problematisch und wichtig?
Ein Beispiel aus dem Buch "Statistik verstehen, nicht rechnen" des Statistikers Frank Siegmann: Stellen wir uns vor, wir sind Personalchef in einem großen Unternehmen und wir hören immer wieder die Kritik, dass wir zu wenig Frauen einstellen. Das ist auf den ersten Blick nicht von der Hand zu weisen, denn im vergangenen Jahr haben wir von 200 weiblichen und 200 männlichen Bewerbern nur 35 Frauen, aber 40 Männer eingestellt. Die Einstellungsquote für Frauen betrug 17,5 Prozent, die für Männer 20 Prozent.
Es gibt in unserem Unternehmen jedoch zwei Sparten, in denen es im vergangenen Jahr Einstellungen gab: im betriebswirtschaftlichen und im technischen Bereich.
- Im technischen Bereich gab es lediglich 40 weibliche Bewerber, von denen zehn eingestellt wurden (eine Quote von 25 Prozent), aber 130 männliche Bewerber, von denen 30 eingestellt wurden (eine Quote von 23,1 Prozent).
- Im betriebswirtschaftlichen Bereich haben sich 160 Frauen beworben und 25 bekamen einen Job (eine Quote von 15,6 Prozent) und ebendort haben sich 70 Männer beworben, von denen 10 eingestellt wurden (14,3 Prozent).
Gemäß der Prozentanteile bezogen auf die Gesamtzahl der Bewerber sieht es so aus, als kämen die Frauen schlechter weg. Wenn man sich aber die Bewerbungen und Einstellungen nach Sektor ansieht, fällt auf, dass die Frauen bevorzugt wurden. Simpson-Paradoxon nennt sich dieses Phänomen, bei dem die Bewertung verschiedener Gruppen unterschiedlich ausfällt, wenn man die Ergebnisse kombiniert – oder eben nicht.
Prozentzahlen können aber auch für sich allein Falsches wiedergeben
Ein Beispiel von Statista zeigt: Eine Partei ABC bejubelt ihre 100-prozentige Erhöhung der Frauenquote. Partei XYZ muss dagegen zugeben, dass ihre Frauenquote nur um 20 Prozent erhöht werden konnte. Klingt so, als müsste sich Partei XYZ mehr anstrengen, was den Frauenanteil angeht. Doch bisher kennen wir die absoluten Zahlen nicht.
"Angenommen, in der Partei ABC waren vier weibliche Abgeordnete und jetzt kommen vier weitere dazu, dann ist die Frauenquote hier tatsächlich um 100 Prozent gestiegen. In der Partei ABC sind nun insgesamt acht Frauen – dies jedoch bei über 100 Abgeordneten. Der Anteil weiblicher Abgeordneter liegt also nur bei acht Prozent.
Partei XYZ hat auch 100 Abgeordnete, darunter aber bereits 40 Frauen, also 40 Prozent. Jetzt kommen acht dazu, also eine Steigerung um 20 Prozent. Wenn Partei XYZ schlau gewesen wäre, hätte sie verkündet, dass sie 100 Prozent mehr weibliche Abgeordnete hinzuzubekommen hat als Partei ABC (nämlich acht statt vier). Oder sie hätte sagen können, dass ihre Fraktion 400 Prozent mehr Frauen in ihren Reihen hat als die Fraktion ABC. All das erkennt man aber erst, wenn man einen Blick auf die absoluten Zahlen wirft.
Absolute Zahlen allein, wenn sie nicht ins Verhältnis gesetzt werden, sind auch oft irreführend
Ein gutes Beispiel dafür sind die Zahlen der Corona-Infizierten in Deutschland. Am 21. September konnten wir im Dashboard des Robert-Koch-Institutes Folgendes nachlesen: München hatte 10.673 ausgewiesene Corona-Fälle, der Landkreis Dachau gleich nebenan verzeichnete 1211 Corona-Fälle. München hatte es schlimmer getroffen – könnte man jetzt meinen, wenn man nur diese beiden Zahlen vergleicht.
Doch man muss in Betracht ziehen, dass in München viel mehr Menschen leben. Rund 1,5 Millionen Einwohner hat München. Die Chance, dass unter so vielen einige Corona haben, ist also viel höher als im Landkreis Dachau, der gerade einmal rund 154.000 Einwohner zählt. Aufschlussreicher ist hier die Zahl der Fälle pro 100.000 Einwohner. Und schaut man sich die an, kommt der Landkreis schlechter weg: 787 Fälle pro 100.000 Einwohner – München hat 725,3 pro 100.000.
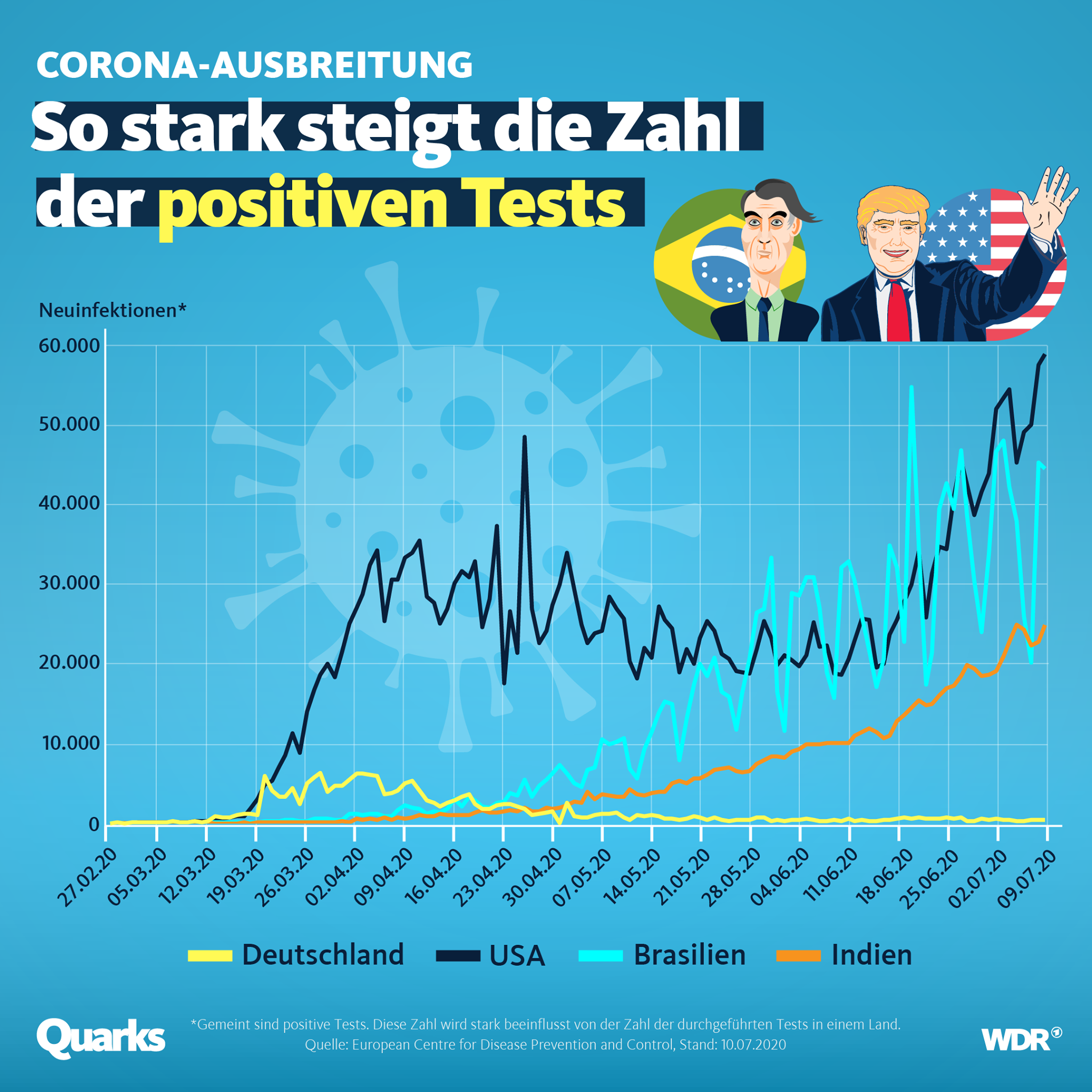
In dieser Grafik haben wir uns beispielsweise dazu entschieden, die absoluten Zahlen der Corona-Neuinfektionen beziehungsweise der positiven Tests zu zeigen. Das haben wir bewusst so getan, damit man einen Eindruck von der schieren Zahl bekommt. Statistisch vergleichbar wird es aber erst, wenn man die Neuinfektionen pro 100.000 Einwohnern pro Land darstellt.
Weitere Angaben zum Artikel:
Statistik kompakt: Was du dir merken solltest
- Die Zielpopulation sollte klar definiert sein.
- Eine Stichprobe sollte zufällig ausgewählt werden (wenn möglich) und groß genug sein (und die Stichprobengröße sollte genannt werden).
- Die Art der Erhebung sollte zum Thema passen (Laborexperiment, Umfrage etc.).
- Wenn eine Umfrage durchgeführt wurde, hilft es, den Wortlaut der Fragen zu kennen.
- Ein "Fehler" ist nicht Schlimmes in der Statistik. Mit einer Fehlergrenze werden Ergebnisse erst richtig transparent.
- Korrelation ist nicht gleich Kausalität.
- Assoziation ist nicht gleich Korrelation.
- Immer an mögliche Störvariablen denken.
Artikel Abschnitt:
Quellenangaben zum Artikel:
Social Sharing:
Artikel Überschrift:





Vielen Dank für den Beitrag, der gut verständlich ist. Noch ein Beispiel: Bei der Massenüberwachung in Berlin durch Kameras mit Gesichtserkennung gab es „nur“ eine Fehlerquote von 0,1 %. Alle waren zufrieden. Doch wenn, diese Überwachung auf allen deutschen Bahnhöfen eingeführt werden würde, müssten – bei 12 Mio. Fahrgästen am… Weiterlesen »
Ein guter Übersichtsartikel.